[leetcode]85. Maximal Rectangle

속도는 느렸지만 Hard 문제를 혼자서 풀었다는점에 점수를 주는 문제입니다.

https://leetcode.com/problems/maximal-rectangle

주어진 matrix 에서 1만으로 구성된 가장큰 rectangle의 넓이를 구하는 문제입니다.

dp[i][j] 를 (i , j)의 가장 긴 가로의 길이로 정의하고 문제를 풀었습니다.

dp[i][j] = dp[i][j-1] +1 , if matrix[i][j] == 1

0 , if matrix[i][j] != 1

이렇게 matrix 안에서 가로의 길이들을 구한뒤에 가로가 만들어질때 위로 한칸씩 가로들을 쌓아 올라가면서 직사각형을 만들어봅니다.

현재 빨간색 지점 ( i,j )에 있다고 할때 현재 row의 가장 긴 가로의 길이를 1차로 구하고 dp 에 저장된 dp[i-1][j] 로 위에 쌓인 가로들의 길이를 찾아서 가로를 쌓아올려 직사각형을 만듭니다.

이렇게 만들어진 직사각형의 넓이를 구하고 현재 찾은 max 넓이 값과 비교해서 정답이 될 수 있다면 max 값을 update 해줍니다.

class Solution(object):
    def maximalRectangle(self, matrix):
        """
        :type matrix: List[List[str]]
        :rtype: int
        """
        # dp[i][j] => i,j 까지의 가로 길이
        R , C = len(matrix) , len(matrix[0])
        dp = [ [0]*C for _ in range(R)]
        result = 0
        for i in range(R):
            for j in range(C):
                if matrix[i][j] == "1" :
                    dp[i][j] = dp[i][j-1] + 1
                    y_val = 1
                    x_val = dp[i][j]
                    
                    while True:
                        result = max(result, x_val*y_val)  
                        if i - y_val < 0 :
                            break
                        if matrix[i- y_val][j] != "1" :
                            break
                        x_val = min(x_val , dp[i - y_val][j] )
                        y_val += 1
                        
                    
        return

class Solution(object):

def maximalRectangle(self, matrix):

"""

:type matrix: List[List[str]]

:rtype: int

"""

# dp[i][j] => i,j 까지의 가로 길이

R , C = len(matrix) , len(matrix[0])

dp = [ [0]*C for _ in range(R)]

result = 0

for i in range(R):

for j in range(C):

if matrix[i][j] == "1" :

dp[i][j] = dp[i][j-1] + 1

y_val = 1

x_val = dp[i][j]

while True:

result = max(result, x_val*y_val)

if i - y_val < 0 :

break

if matrix[i- y_val][j] != "1" :

break

x_val = min(x_val , dp[i - y_val][j] )

y_val += 1

return

제가 접근한 방법의 가장 큰 문제는 각 point 를 접근할때마다 다시 한번 위로 올라가면서 가능한 모든 경우의 수를 확인하기 때문에 O( M + N^2) 의 시간복잡도를 가지게 됩니다.

실제 결과도 pass는 했지만 굉장히 느린 속도였습니다.

사각형을 하나씩 쌓아올린다는 접근법은 생각하기는 쉬웠으나, 중복 계산으로 인해 성능에 문제가 있네요.

이번에 chatGPT plus 를 사용하게되면서 GPT4에게 한번 물어보았습니다.

(GPT3는 HARD 문제를 잘 풀지 못했습니다.)

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        if not matrix or not matrix[0]:
            return 0
        
        m, n = len(matrix), len(matrix[0])
        heights = [0] * (n + 1)
        max_area = 0
        
        for i in range(m):
            for j in range(n):
                heights[j] = heights[j] + 1 if matrix[i][j] == "1" else 0
            
            stack = [-1]
            for j in range(n + 1):
                while heights[j] < heights[stack[-1]]:
                    height = heights[stack.pop()]
                    width = j - 1 - stack[-1]
                    max_area = max(max_area, height * width)
                stack.append(j)
        
        return max_area

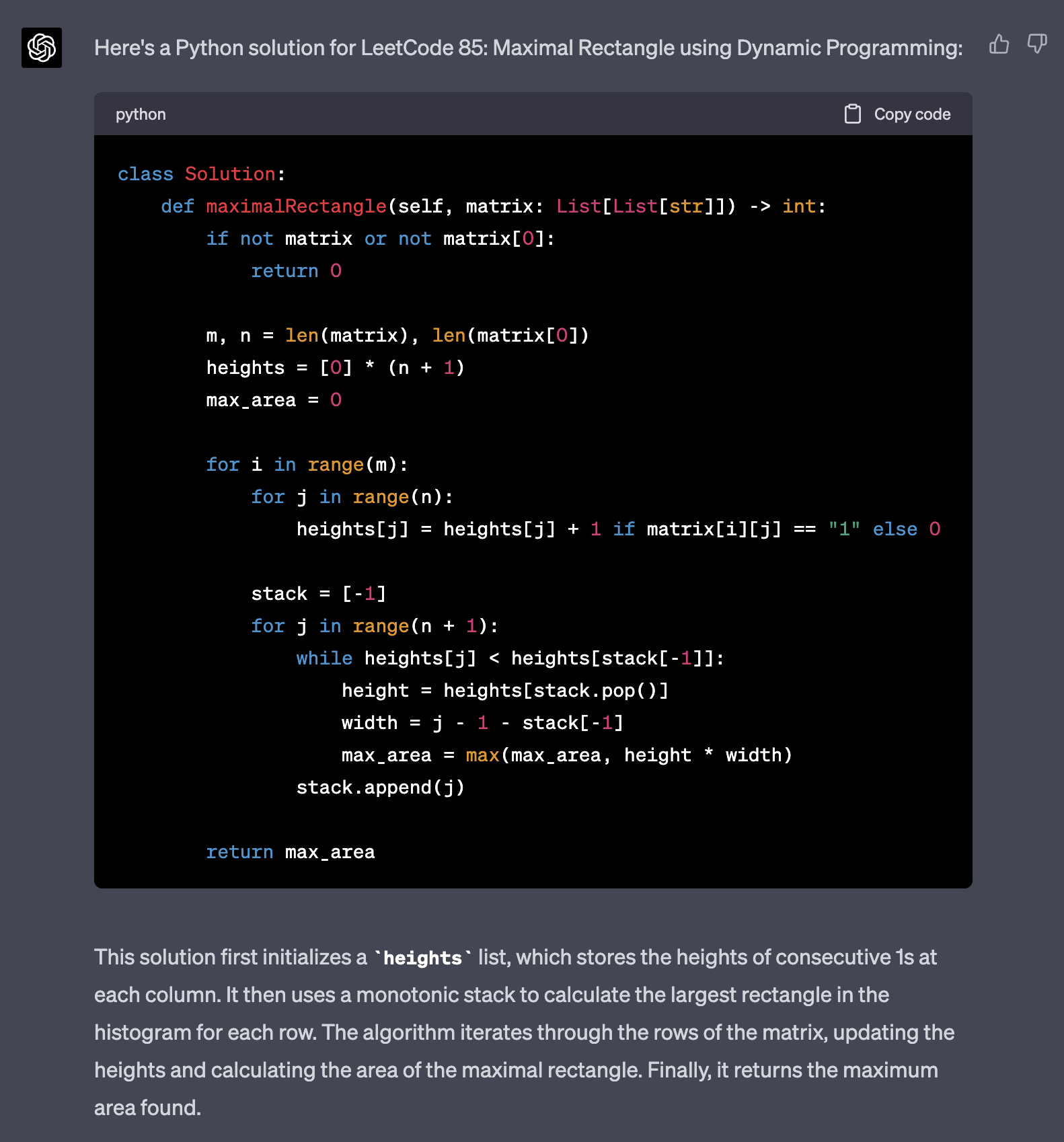
class Solution:

def maximalRectangle(self, matrix: List[List[str]]) -> int:

if not matrix or not matrix[0]:

return 0

m, n = len(matrix), len(matrix[0])

heights = [0] * (n + 1)

max_area = 0

for i in range(m):

for j in range(n):

heights[j] = heights[j] + 1 if matrix[i][j] == "1" else 0

stack = [-1]

for j in range(n + 1):

while heights[j] < heights[stack[-1]]:

height = heights[stack.pop()]

width = j - 1 - stack[-1]

max_area = max(max_area, height * width)

stack.append(j)

return max_area

가장 놀라운건 성능인것 같습니다.

제 코드가 100명 중에 90 등이면, GPT4의 코드는 3등이네요.

chatGPT 가 제공한 solution 을 살펴보면 O(N+M) 의 시간 복잡도를 가지는 코드인데요.

우선 row 별로 loop를 돌면서 현재 row에서 가능한 column 별 height 를 관리합니다.

for j in range(n): 
    heights[j] = heights[j] + 1 if matrix[i][j] == "1" else 0

1 2	for j in range(n): heights[j] = heights[j] + 1 if matrix[i][j] == "1" else 0

그리고 height가 바뀌는 지점에서 height * width 를 계산해서 결과값을 찾아봅니다.

for j in range(n + 1): 
    while heights[j] < heights[stack[-1]]: 
        height = heights[stack.pop()] 
        width = j - 1 - stack[-1] 
        max_area = max(max_area, height * width)

for j in range(n + 1):

while heights[j] < heights[stack[-1]]:

height = heights[stack.pop()]

width = j - 1 - stack[-1]

max_area = max(max_area, height * width)

stack 의 값은 pointer 처럼 현재 row의 0번째 index 부터 마지막 index까지 탐색해 나가는데,

height 가 변경된 지점은 pop 처리해서 width를 구할 수 있도록 도와줍니다.

이 알고리즘의 가장 중요한 point 는

heights = [0] * (n + 1)

이라고 생각합니다.

heights를 관리할때 column 사이즈보다 +1 로 관리하면서 마지막에 0으로 채워진 column 을 하나 추가합니다.

column size +1 을 통해서 row의 마지막 width를 계산할 수 있게 되어 정답을 찾을 수 있습니다.

아쉽지만, 저는 아직 chatGPT 가 제공한 solution 처럼 접근할 수 있는 역량이 안됩니다.

하지만, 다양한 문제를 풀어보면서 chatGPT든, 다른 사람들의 코드든 여러 접근 방법에 대해 고민하고 생각을 넓혀 나가야할 것 같습니다.